When initially looking at reaction we often assume that they "go to completion". That is to say that as much product is formed as it allowed by the reactants that are given. In reality most reactions do not go to 100% completion. Instead they reach a point of minimum free energy that is a mixture of reactants and products. This point is called the equilibrium point. At equilibrium the reaction has not stopped, but rather the forward reaction and backward reaction are occurring at the same rate so there is no net change in the concentration of the reactants and products.
Why then do we teach that some reactions "go to completion"? For many reactions, this is very nearly the case. If only one in a few trillion molecules doesn't react, it is not worth talking about the equilibrium. But for many chemical processes even very small amounts of reactants (or left over starting material) are of interest and thus even at these extremes, we are often interested in the equilibrium concentrations.
Here is a nice TED-Ed video on an important chemical reaction and its equilibrium, the formation of ammonia
At equilibrium there is a relationship between the concentrations (partial pressures) of the products and the reactants. We will see that these are the concentration that minimize the total free energy. But for now we will simply invoke this idea. For different types of chemical species, the free energy at equilibrium is related to different standard states. As such, we end up with different "types" of equilibrium constants. This idea can be unified by using a new term which has different definitions in different contexts. This is the "activity." The activity of a compound tells us how the free energy (or more correctly the chemical potential) of that compound varies with the reaction. The equilibrium constant is then a ratio of the activities of the products and the reactants. The activity of each chemical species is raised to the power of its stoichiometric coefficient in the balanced equations. Therefore, to be interpreted, an equilibrium constant must always be accompanied by a corresponding balanced equation. For example, look at the generic reaction of
\[ a{\rm A} + b{\rm B} \rightleftharpoons c{\rm C} + d{\rm D} \]
for this reaction the equilibrium constant will be
\[ K = {{{a_{\rm C}^c \; a_{\rm D}^d}\over a_{\rm A}^a \; a_{\rm B}^b} }\]
where \(a_{\rm i}\) is the activity of compound i. The expression on the right is the mass action expression (or law of mass action). Technically the "law of mass action" states that at equilibrium this expression is a constant. We typically referred to this constant as the equilibrium constant. This ratio of the activities at equilibrium gives us the value of the equilibrium constant. At any other conditions, these activities are simply the activities "now" and we give the mass action expression a different name "the reaction quotient", generally denoted by the a capital Q.
To give a concrete example, let's look at the reaction
\[\rm{2H_2(g)+O_2(g) \rightleftharpoons 2H_2O(g)}\]
the equilibrium constant for this reaction will be
\[K = {{a_{\rm H_2O}^2} \over {a_{\rm H_2}^2 \; a_{\rm O_2}}}\]
The activity of a chemical species varies depending on its phase (since the free energy will change differently in different phases during a reaction). For gases the activity is defined as
\[a_i = {P_i \over P^{\circ}}\]
where \(P^{\circ}\) is the standard pressure of 1 atm (or 1 bar). This means that the activity is simply the partial pressure in atm, but since we divide by one atm the activity is unit less.
For solutions, the activity is nearly identical except that it is the concentration
\[a_i = {[i] \over C^{\circ}}\]
where the standard concentration, \(C^{\circ}\) is just 1 M. So the activity is simply the concentration in Molarity (but since it is divided by 1 M it is also unit less).
For pure solids and pure liquids the free energy doesn't change from the standard value during a reaction and thus the activity is just defined as 1.
\[a_i = 1\]
So anywhere we have the activity of a solid or a liquid in the equilibrium expression it "disappears" since it is replaced by the number 1.
For example the equilibrium constant for the reaction
\[\rm{CaCO_3(s) \rightleftharpoons CaO(s) + CO_2(g)}\]
is
\[ K = {{a_{\rm CaO(s)} \; a_{\rm CO_2(g)}} \over {a_{\rm CaCO_3(s)}}} = P_{\rm CO_2}\]
Any example of an aqueous equilibrium is
\[\rm{HF(aq) + H_2O(l) \rightleftharpoons H_3O^+(aq) + F^-(aq)}\]
for which the equilibrium constant would be
\[ K = {{a_{\rm F^-(aq)} \; a_{\rm H_3O^+(aq)}} \over {a_{\rm HF(aq)} \;{a_{\rm H_2O(l)} }}} ={{{\rm [F^-]} \; {\rm [H_3O^+]}} \over {{\rm [HF]}}} \]
The equilibrium constant is related to the concentration (partial pressures) of the products divided by the reactants. So if the equilibrium constant is larger than 1, there will be "more products" at equilibrium. If it is less than 1, there will be more reactants. This is a qualitative idea as the concentrations are often raised to various powers and it depends on the number of chemical species in the reaction. None the less, this is a very valuable idea.
When K > 1 we say a reaction "favors the products".
When K < 1 we say it "favors the reactants".
It is important to note that K can be very very large (like 1058 large) or very very small (10-27) small. (Those are just random big and small numbers.)
While the equilibrium constant is fixed, there are an infinite number of combinations of concentrations that results in the same ratio. That means for any given reaction, the concentration at equilibrium will depend on the starting conditions. However, at equilibrium we'll have the same ratio.
For example for a reaction
\[{\rm A + B \rightleftharpoons C}\]
we can take the equilibrium constant to be 100. There are many possibilities that could give this result.
[A] = 1 M, [B] = 10-2M , [C] = 1 M
[A] = 10-2M, [B] = 1 M, [C] = 1M
[A] = 1 M, [B] = 10-4, [C] = 10-2M
In all of these cases, if we plug the values into the equilibrium constant we get 100. However, they are all very different. In the third case, it would be hard to say there is "more product" even though this reaction favors the product.
Often we have an equilibrium constant for a particular reaction, but we would like it for a different reaction. In the same way that we can add or subtract reactions from one another we can manipulate equilibrium constants.
If we want the K for a reaction that is the reverse of reaction that is given
\[{\rm A + B \rightleftharpoons C } \hskip 24pt K_{\rm forward}\]
\[{\rm C \rightleftharpoons A + B } \hskip 24pt K_{\rm reverse} = 1/K_{\rm forward}\]
For a reaction that you double the stoichiometric coefficients, the equilibrium constant is squared
\[{\rm A + B \rightleftharpoons C} \hskip 24pt K_1=K\]
\[{\rm 2A + 2B \rightleftharpoons 2C} \hskip 24pt K_2=K^2\]
If we add two reactions, the equilibrium constant for the total reaction is the product of the equilibrium constants for the two reactions we added together.
\[{\rm A + B \rightleftharpoons C} \hskip 24 pt K_1\]
\[{\rm C \rightleftharpoons D} \hskip 24 pt K_2\]
\[{\rm A + B \rightleftharpoons D} \hskip 24 pt K = K_1 \; K_2\]
For a reaction involving gases, we should use the equilibrium constant with partial pressures if we want to relate this constant to the thermodynamic energies. However, we can solve equilibrium problems for gases with a constant written in terms of concentrations. To keep these two straight (since they are unit less) we give them different notations. The equilibrium constant with pressures is Kp and the equilibrium constant with concentrations is Kc. These two are related since both depend on the number of moles of each chemical species. This is easiest to see for a given reaction. Look at the reaction
\[\rm 2H_2(g) + O_2(g) \rightleftharpoons 2H_2O(g)\]
\[K_p = {P_{H_2O}^2 \over {P_{H_2}^2 \; P_{O_2}}}\]
writing the partial pressure in terms of the number of moles of each species we get
\[K_p = {{n_{H_2O}RT \over V}^2 \over {n_{H_2}RT \over V}^2 \; {n_{O_2}RT \over V}}\]
Since the concentration for each species is given by the number of moles divided by the volume, you can see this appears in the given expression. The partial pressure is simply the molar concentration times a factor of RT. For this reaction, if we gather all the concentrations together you can see we have
\[K_p = {{{n_{H_2O} \over V}^2 \over {n_{H_2} \over V}^2 \; {n_{O_2} \over V}} \times {1 \over RT}} = {K_c \times {1 \over RT}}\]
So you can see that Kp is related to Kc by a factor of RT. This factor depends on the number of moles of gas in the products compared to the reactants. If they have the same number of moles of gas then Kp = Kc. Otherwise
\[K_p = K_c(RT)^{\Delta n}\]
where \(\Delta n\) is the change in the number of moles of gas (products - reactants). For the example reaction, there are three moles of gas in the reactants and two moles of gas in the products so \(\Delta n\) is negative one.
A video that shows the differences in Kc and KpFor the reaction, H2(g) + I2(g) forming 2HI(g) which equilibrium constant would be larger?
Systems move to equilibrium because that is the point at which the reaction mixture has the lowest free energy. The free energy depends both on the compounds (what are the reactants and products) as well as the concentrations of the mixture. We can think of this as breaking down into two parts.
\[\Delta G_{\rm r} = \Delta G_{\rm r}^{\circ} + RT\ln Q\]
where this is the instantaneous difference in free energy between reactants and products at any given set of concentrations. This \(\Delta G_{\rm r}\) depends on two terms. The first is the standard free energy difference. This is the one we calculate from all of our tabulated data. It is a comparison between pure products (in their standard state 1 atm or 1M) and pure reactants (in their standard state 1 atm or 1 M). So if \(\Delta G_{\rm r}^{\circ}\) is negative, the products are lower in free energy and if it is positive, then reactants are lower. However, the point of the very lowest free energy is always somewhere in between these two. This is because some mixing always lowers the free energy (increased mixing leads to higher entropy leading to lower free energy). So the equilibrium point is always somewhere in between these two extremes. The more negative the standard free energy the closer the point will be towards all products, the more positive it is the closer this point is towards all reactants.
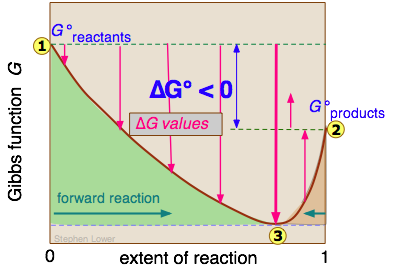
For example this diagram shows a reaction for which \(\Delta G_{\rm r}^{\circ}\) is negative so it "favors" the products.
This is a plot of the Gibbs free energy (labeled as the Gibbs Function) versus the extent of the reaction. When the extent of the reaction is zero, the mixture is 100% reactant molecules. When the extent of the reaction is one, the mixture is 100% product molecules. Point 1 on the graph is the Gibbs Free energy of the reactant molecules in their standard states and point 2 is the free energy of the products in the their standard state. The difference between these two is \(\Delta G_{\rm r}^{\circ}\). Since the products are lower in free energy, we know the equilibrium will lie towards the products. The minimum in free energy is the equilibrium point labeled 3. The larger \(\Delta G_{\rm r}^{\circ}\) is, the closer this point will be toward the reaction going to all products. Conversely if \(\Delta G_{\rm r}^{\circ}\) is positive the equilibrium will be on the reactant side as shown below.
For both of these plots, all of the various mixtures that lie between points 1 and 3 are reactant heavy (where \(Q\lt K\)) and the reaction will thus proceed forward, making more products. This allows the system to continue to decrease the overall free energy of the system until equilibrium is reached at the bottom of the "free energy well". Conversely, all of the mixtures that lie between points 3 and 2 are product heavy (where \(Q\gt K\)). All of those mixtures will therefore react by going backwards (to the left) which allows the free energy to drop back to the minimum state at the equilibrium position which is always at the bottom of the "well".
Both \(Q\) and \(K\) are written as the "mass action expression" that is the activities of the products (raised to their powers) divided by the activities of the reactants (raised to their powers).
Previously, we saw that the free energy depended on the standard reaction free energy \(\Delta G_r^{\circ}\) as well as the concentrations (pressures) of the mixtures due to the mass action expression.
At any given instant the free energy difference is
\[\Delta G_{\rm r} = \Delta G_{\rm r}^{\circ} + RT\ln Q\]
Equilibrium will be at the point where \(\Delta G_{\rm r}\) is zero. At this point then \(\Delta G_{\rm r}^{\circ}\) and \(RT\ln Q\) will be equal but opposite in sign. Since this is the equilibrium point, the mass action expression that we were calling \(Q\) will now have not just any values but will have the equilibrium value. This is what we are calling \(K\). Combining these ideas we get
\[\Delta G_{\rm r}^{\circ} = -RT\ln K\]
That is the equilibrium point depends on the standard Gibb's Energy for the reaction. We can rearrange to solve for \(K\) and get
\[K = \exp \left(-{\Delta G_{\rm r}^{\circ} \over RT}\right)\]
So if the standard reaction free energy is negative, then \(K\) will be a number greater than one (favor the products) and if it is positive \(K\) will be less than one (favor the reactants). In the odd case the standard reaction free energy is zero \(K\) will be equal to one.
The larger in magnitude \(\Delta G_{\rm r}^{\circ}\) is the more extreme it will be. Very negative standard reaction free energies will make for very large \(K\)'s (essentially 100% completion of the reaction as written). Very positive standard reaction free energies will lead to extremely small \(K\)'s (essentially no reaction as written).
Q and K often get mixed up since they have the same form. They are both state functions, the difference is K is the value of the mass action expression (the concentrations or pressures of the products over the reactants) when those concentrations (or pressures) are the values at equilibrium. Q is the value we get any point away from equilibrium. Thus if you are trying to figure out if you are at equilibrium (and if not, which way the reaction will shift to get to equilibrium) you first need to calculate Q and compare it to K.
K is a fixed number. It depends on ΔGr°. Q can be anything. It depends on the concentrations right now (state function). So if you have a given mixture, simply put the concentrations (pressures) into the mass action expression and find Q. Then compare Q to K.
If Q > K then the equilibrium "lies towards the reactants". This is because there are "too many products". The mass action expression is products over reactants. If Q is too big you need to get rid of products and form more reactants. This is not a choice. It is simply a way to express that the point of lowest free energy (the equilibrium) is a mixture that contains more reactants and less products (a smaller value of the mass action expression).
If Q < K the opposite is true. The mass action expression is "too small". That is there are too many reactants. Equilibrium lies at a point with higher concentrations of products. So the equilibrium lies to right and the reaction will proceed toward the products.
The reaction will continue to change until the point where the value of Q reaches the one value it can have a equilibrium, K. Then when you calculate Q for what you have "now", you'll find it is exactly equal to K and you can conclude you are in fact at equilibrium.
Le Chatelier's Principle is an idea about how a reaction mixture that is at equilibrium will react when it is perturbed away from equilibrium. This is a general idea that can help us to quickly have some insight into chemical equilibria and change.
Le Chatelier's Principle states
If a chemical system at equilibrium experiences a change, then the equilibrium shifts to counteract the imposed change and a new equilibrium is established.
By "change" we are moving the system away from equilibrium such that Q ≠ K. We can understand the direct the system need to move to re-establish equilibrium by thinking about what happens to Q when we "stress" or "change" the system.
We will deal with three particular examples.
Here are a couple of Le Chatelier's Principle diagrams for you to use and help you "visualize" the concept. Click on the images below to see a bigger version. One is a doodled thing with comments, the other a flow chart.
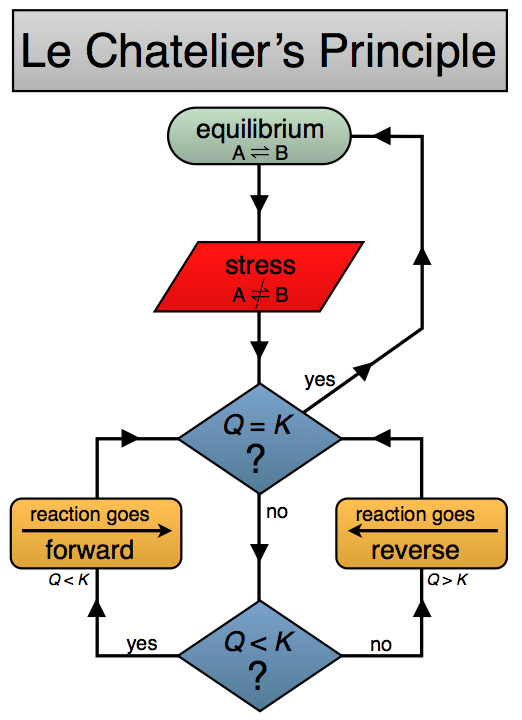
If a reaction mixture is at equilibrium, if you add some more reactant, according the Le Chatelier's principle than the reaction will change in order to "counteract" the change. That is to say is will shift to partially "undo" the change you have made. Therefore if reactants are added, the reaction shifts to "remove" some reactants. This can be accomplished by shifting towards the products and forming more products. Conversely if you add products, the reaction will shift to reactants to counteract this change.
While Le Chatelier's principle is handy (and correct), it can often give the wrong impression especially as one tries to explain it. It makes it seem like the reaction mixture is making some sort of decision of what to do. Moreover, without understanding the underlying ideas you can arrive at the wrong answers. This first idea of adding (removing) products or reactants is not different than Q vs K. When a reaction is at equilibrium, the mass action expression (the concentrations of the products divided by the concentration of the reactants) has a value equal to K (Q = K). If you change those concentration you will no longer be at equilibrium (Q ≠ K).
\[Q = {Products \over Reactants}\]
Adding reactants (or removing products) will lead to a situation in which Q < K (you're dividing by a bigger number). Adding products (or removing reactants) will lead to Q > K (you'll have larger number on top of the mass action expression).
It is important to make this connection since pure liquids and pure solids have activities that are one (they don't appear in the mass action expression). Thus if you add more of them they will not affect the equilibrium at all. Solubility is a situation like this. If you have a saturated solution and you add more solid nothing happens (the reaction does not shift to the right even though you have added more reactant). You need to change the concentrations or pressures in the mass action expression to affect the equilibrium.
Finally, in solution, it is possible to change the concentration of all the species at the same time by adding more solvent (or evaporating some solvent). If you dilute a solution by adding solvent, all of the concentrations will decrease. This will potentially change Q. If there are more species in solution that are products than reactants then Q will decrease. The reaction will then shift back towards the product side to reach equilibrium. If there are more species in solution that are reactants than products, then Q will increase upon dilution and the reaction will shift back towards the reactant side. When you dilute a reaction at equilibrium the reaction will shift in such a way to increase the total concentration (this means moving towards the side of the reaction with a greater number of species in solution). If you remove solvent, you concentrate the solution. Then the reaction will shift toward the side with the fewest number of species in solution.
A video on LeChatelier's PrincipleChanging the volume of the container with a reaction mixture is essentially only possible for a reaction involving gases.
First, let's look at Le Chatelier's principle. If we mechanically decrease the volume of a container of gases the pressure inside the container will increase. Le Chatelier's principle tells us the reaction will re-achieve equilibrium by shifting to counteract this change. Since the change we made was to increase the pressures the reaction will shift in such a way to decrease the pressures. This can be achieved by moving towards the side of the reaction with fewer gas molecules.
Two key ideas to note. First, this is only an effect for reactions that involve gases. Second, the volume only affects reactions that have different numbers of moles of gas in the products and reactants. Why is this? It is again Q vs K. It is easier to see if we look at an example reaction. Let's take
\[{\rm 2NO_2(g) \rightleftharpoons N_2O_4(g)}\]
For this reaction
\[Q = {P_{\rm N_2O_4} \over P_{\rm NO_2}^2}\]
So, if you increase the pressure by decreasing the volume, the partial pressures will increase. Since the reactants have two moles of gas, the pressures of the reactants are squared. This means that the effect will be larger for the reactants. Dividing by a bigger number will make Q smaller and you'll find that after increasing the pressures Q < K. Then equilibrium is towards the products side. This is the side with fewer molecules.
Similarly if we mechanically increase the volume of a container, the pressure of the gas inside the container will decrease. Now the system will re-establish equilibrium by shifting to side of the reaction with the greatest number of moles of gas.
If the reaction has the same number of moles of gas in the reactants and products (\(K_{\rm p} = K_{\rm c}\)) then volume (pressure) will have no effect.
Finally, sometimes the volume is increased by adding an inert gas to the mixture at constant pressure. In this case the total pressure will stay constant, but the partial pressures of the reactants and products will decrease. This is because the total pressure now includes the pressure resulting from the inert gas. This has the effect of diluting the mixture and is identical to simply mechanically increasing the volume.
Increasing the pressure by adding an inert gas at constant volume has no effect. This is because what matters for the equilibrium are the partial pressures of the reactants and products. Adding an inert component to a system at constant volume will change the total pressure but not the partial pressures of the compounds of interest.
For reactions in the solution, you can have identical effects by changing the total volume of the solution. Adding water will effectively dilute all the concentrations. The reaction will then shift to counter this by moving toward the side of the reaction with more aqueous species in solution. Conversely concentration the solution lowers the volume and raises the concentrations. This will cause the reaction to shift to the side with fewer aqueous species. It follows the identical reasoning to the Q vs K examples given above except that the mass action quotient has concentrations instead of partial pressures.
The last change for Le Chatelier is to change the temperature. We can understand this by looking at the enthalpy change for a reaction and thinking about the reaction as either producing or consuming "heat" as a result of the reaction.
For an exothermic reaction
\[{\rm reactants \rightleftharpoons products + heat}\]
So "heat" is a product. If you raise the temperature (by inputting energy in the form of heat) then the reaction will "counteract" this by shifting to the reactant side. The converse is true of endothermic reactions
\[{\rm reactant + heat \rightleftharpoons products} \]
Now adding heat is like adding a reactant, the reaction shifts towards the products.
Why is this?
The reason here is quite different than for the previous examples since what is changing is the value of the equilibrium constant. The value of the equilibrium constant depends on temperature for two reasons.
\[\Delta G_{\rm r}^{\circ} = -RT\ln K\]
There is a factor of the temperature in the relationship between the standard free energy and K. In addition, the standard free energy depends on temperature.
\[\Delta G_{\rm r}^{\circ} =\Delta H_{\rm r}^{\circ} -T\Delta S_{\rm r}^{\circ}\]
combining these two we see that
\[-RT\ln K = \Delta H_{\rm r}^{\circ} -T\Delta S_{\rm r}^{\circ}\]
\[\ln K = {\Delta H_{\rm r}^{\circ} \over -RT} + {\Delta S_{\rm r}^{\circ} \over R}\]
\[ K = {exp\left({-\Delta H_{\rm r}^{\circ} \over RT}\right) \times constant}\]
So we can see that \(K\) (or the \(\ln K\)) has a temperature dependence that depends on the value of \(\Delta H_{\rm r}^{\circ}\) (its the term with the \(T\) in the resulting formula). The constant in the expression depends on the value of \(\Delta S_{\rm r}^{\circ}\).
So \(K\) has a strong dependence on temperature. Moreover, the sign of the change depends on the sign of \(\Delta H_{\rm r}^{\circ}\). If the standard reaction enthalpy is positive (endothermic) then as \(T\) increases \(K\) increase (more products at equilibrium than before). For exothermic reactions, as \(T\) increases \(K\) decreases (more reactants at equilibrium than at the previous temperature).
Often this is misinterpreted that endothermic reactions require high temperatures to be spontaneous. It is simply that at higher temperatures, endothermic reactions shift to the right.
This provides a lot of useful insight into typical chemical processes. Often it can be hard to look at a reaction and know if it is endothermic or exothermic. But bond breaking requires energy (endothermic) and bond formation releases energy (exothermic). So very often decomposition reactions where one compound breaks apart into two (or more) typically have more bond breaking than forming and tend to be endothermic. So for example, if you have rust (iron oxide \(Fe_2O_3\)) and you'd like to make iron metal
\[{\rm 2Fe_2O_3(s) \rightleftharpoons 4Fe(s) + 3O_2(g)} \]
At room temperature the equilibrium constant for this reaction is extremely small. So the equilibrium is essentially all reactants. However, this reaction is endothermic (like most decompositions). So if you want to increase the value of K you can raise the temperature. Thus to make rust into iron spontaneously, you can get the temperature very high and the equilibrium will shift to the right. This is the process of "smelting" iron ore.
The temperature dependence of K has one final application. For many reactions, it can be very difficult to measure if they are endothermic or exothermic (since the amounts of materials might be extremely small). However, we can often measure concentrations. So there are situations in which we measure the temperature dependence of \(K\) to determine \(\Delta H_{\rm r}^{\circ}\). In this way we can try to put a number to \(\Delta H_{\rm r}^{\circ}\) either by measuring heats (calorimetry) or concentrations (equilibria).
A video explaining the relationship of Temperature Change and LeChatelier's Principle. Which way will the reaction shift when temperature is increased? decreased?In the last section we showed how K is dependent on T and ΔH. The derived equation was
\[ K = {exp\left({-\Delta H_{\rm r}^{\circ} \over RT}\right) \times constant}\]
There is a very convenient formula that will allow us to factor out the constant that comes from entropy. By setting up this equation under two conditions (1 and 2) one can arrive with the following familiar equation:
\[\ln\left({K_2\over K_1}\right) = {\Delta H\over R}\left({1\over T_1}-{1\over T_2}\right)\]
So why is this familiar? This is a close copy of the Claussius-Clapeyron equation which related vapor pressure and the heat of vaporization. This version relates K's at two different temperatures and is known as the van't Hoff equation.
When you really think about it, the Claussius-Clapeyron equation is just a special case version of the van't Hoff equation. The van't Hoff deals with an equilibrium condition in a general sense while the Claussius-Clapeyron equation is a very specific case of liquid/gas physical equilibria.
Unlike the Claussius-Clapeyron equation, the van't Hoff equation can have either positive or negative &DeltaH. Because chemical reactions can be endothermic(+) or exothermic(-), K can go up or down with temperature changes. After checking the math, you will find that increasing the temperature of an endothermic reaction will lead to an increase in the value of K. The opposite is true for exothermic reactions.
When a chemical system is out of equilibrium we typically want to figure how exactly it will get to equilibrium and what all the new equilibrium concentrations and/or pressures will be. We treat this problem in a methodical way. This method is actually just "doing the algebra" to get your answer. You should practice this method over and over until it feels like your doing what is obvious. Let's get started.
First, we will assume that you have a system that is not at equilibrium and Q does not equal K. The reaction is poised to go forward or backwards in order to reach the desired equilibrium state. The problem is we do not know how much it goes forward or backwards - that is the unknown part and will be the part we use algebra to solve. Our unknown amount that reacts will be our x. We have a big advantage on our side though, we know exactly how each species reacts relative to each other. This is known as stoichiometry and is a major part of all chemistry classes. Time to flex your stoichiometry muscle so to speak.
So what is RICE? It's an acronym where each letter identifies a line in a table. The top line is the reaction itself - the R. The next line is the initial conditions of concentration or pressure - the I. The third line is the amount that reacts which we call the change line - the C. And finally on line four we write out the actual equilibrium amounts - the E. All together that is RICE and you've made a RICE table to help you "see" the stoichiometry in a very systematic/methodical way.
Example:
Consider the simple reaction: \({\rm A\;+\;B\;\rightleftharpoons \; 2C}\)
The stoichiometry is simple, one mole of A will react with one mole of B to form two moles of C. Also given with this reaction is the fact that K = 4. So the final equilibrium condition has to satisfy the condition that the mass action expression calculates out to be 4. Now we need an initial condition. For this example lets have 0.10 M A, 0.10&nbps;M B, and no C present. This is a condition where Q is zero and therefore the reaction must go forward to make some C. The RICE table will help. Here is the table the way you should create it.
| R : | A | + | B | \(\rightleftharpoons\) | 2C |
|---|---|---|---|---|---|
| I : | \(0.1\) | \(0.1\) | 0 | ||
| C : | \(-x\) | \(-x\) | \(+2x\) | ||
| E : | \(0.1-x\) | \(0.1-x\) | \(2x\) |
Note how we handle the "unknown" amount by writing \(-x\) for how much A and B you react and \(+2x\) for how much C you make. The x-terms on the change or C-line will always match the stoichiometry in the reaction. This means you will pull down the associated coefficients for each term in your RICE table. The rest is just correctly substituting the equilibrium values back into the mass action expression and then solving for \(x\).
\[K = {[\rm C]^2\over [\rm A][\rm B]}\] \[4 = {(2x)^2\over (0.1-x)(0.1-x)} = {(2x)^2 \over (0.1-x)^2}\]
Now we solve for \(x\). First we take the square root of both sides and get:
\[2 = {2x\over 0.1-x} \] \[0.2 - 2x = 2x\] \[0.2 = 4x\] \[0.05 = x\]
Now we can use our newly found value of \(x\) to calculate the equilibrium concentration of all species - the E-line. A and B are both equal to 0.1-x which means they both decrease down to 0.05 M. The concentration of C is \(2x\) or 2(0.05) which is 0.10 M. We now know all the equilibrium concentrations.
Final Check... We can check and see if these concentrations indeed do calculate out to equal K
\[K = {[\rm C]^2\over [\rm A][\rm B]}\] \[{(0.10)^2\over (0.05)(0.05)} = {0.01 \over 0.0025} = 4\]
Of course 4 = K, so it checks out!
You will use this method over and over to solve various equilibrium problems of all sorts. Practice the method and you will get better at it.