What is the protonation state?

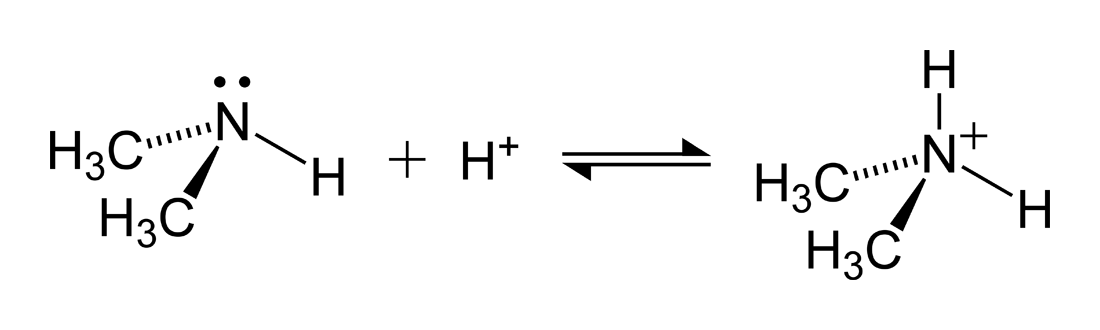
A key idea to consider with any acid/base conjugate pair is the "protonation state" at a given pH.

That is, if you find the molecule in solution at a particular pH, is the proton "on" the molecule (in the protonated form) or "off" the molecule (in the deprotonated form)?

For example, let's consider ammonia

Ammonia, NH₃ is a base and its conjugate acid is the ammonium ion, NH₄⁺. These are essentially two forms of the same compound. One that is deprotonated, the ammonia. One that is protonated, the ammonium. If this compound is found in solution at a particular pH it is important to know which concentration will be larger. This can be deduced by examining the equilibrium constant. As both the protonated form and deprotonated form are in the equilibrium express K_a and K_b either could be used to examine the relationship. We will look at K_a. For the NH₃/NH₄⁺ pair K_a is

\[\rm{K_a ={{[H_3O^+][NH_3]} \over [NH_4^+]} = {[H_3O^+] \times {[NH_3]} \over [NH_4^+]}}\]

K_a has a fixed value. For NH₄⁺ it is 5.56 x 10^-10. What is important is that it is a constant. We are interested in the ratio of the deprotonated form to the protonated form ([NH₃]/[NH₄⁺]. We are considering a solution with a given pH, which means that the [H₃O⁺] is known. Since the product of the [H₃O⁺] and the ratio [NH₃]/[NH₄⁺] is a constant, the larger the [H₃O⁺] the smaller the ratio. This means the [H₃O⁺] increases as the amount of the protonated form increases relative to the deprotonated form. We could have easily determined this from the application of LeChatelier's Principle. Since we know K_a we can determine this relationship quantitatively. Taking the log of both sides of the equilibrium expression yields

\[ \begin{aligned} {\rm log(K_a) = log \left({[H_3O^+] \times {[NH_3] \over [NH_4^+]}} \right) \\ log(K_a) = log([H_3O^+]) + log \left({[NH_3] \over [NH_4^+]} \right) \\ -pK_a = -pH + log \left({[NH_3] \over [NH_4^+]} \right) }\end{aligned}\]

Multiply through by a negative sign (and inverting the logarithm) yields.

\[ \begin{aligned} {\rm pK_a = pH + log \left({[NH_4^+] \over [NH_3]} \right) \\ pK_a - pH = log \left({[NH_4^+] \over [NH_3]} \right) }\end{aligned}\]

Therefore the ratio of the concentration of the protonated form to the deprotonated form depends on the pH compared to the pK_a. A very important condition exists when the pH = pK_a. Then the difference between the two will be zero implying that the ratio of the two species are equal. When the pH = pK_a the solution will contain equal concentrations of both the protonated and deprotonated forms of the compound. What will the ratio be at other pH values? This can be deduced from the formula, but it is easier to simply think about. When the pH < pK_a the solution is "more acidic". The excess protons will protonate the compound and the concentration of the protonated form will be larger than the concentration of the deprotonated form. Similarly if the pH > pK_a the solution is "more basic". This will "pull" the protons off the compound and the concentration of the deprotonated form will be larger than that of the protonated form.

\[ \begin{aligned} {\rm pH = pK_a \;\;\;\; [protonated]=[deprotonated] \\ pH < pK_a \;\;\;\; [protonated]>[deprotonated] \\ pH > pK_a \;\;\;\; [protonated]<[deprotonated] } \end{aligned}\]

This has many implications for chemistry in aqueous solutions (especially for biochemistry). Interactions of molecules and solubility are greatly affected by their charge state. As we protonate or deprotonate compounds their charges, interactions, and solubility will all be changing. The solubility of drug compounds can change dramatically as the pH changes as charged compounds tend to stay in solution (blood) while neutral molecules are absorbed into tissue. This can affect how they are taken up by different regions of the body. Or dramatic difference in drug compounds given orally vs intravenously since stomach acid is dramatically more acidic than blood. Similarly, the structure of proteins can be altered by changing the protonation state of amino-acid residues. As a consequence, the pH in biochemical systems is carefully buffered to be maintained at particular values as fluctuations in pH would have large consequences on protein structure and function.

Polyprotic Acids

Polyprotic acids are acids with more than one acidic proton.  There is a specific equilibrium for each proton coming off of the acid.  The equilibrium constants for these protons are ranked by strength. Often the strengths of each proton are well separated, but for many compounds there are multiple protons with very similar equilibrium states.

The equilibria for polyprotic acids are very simply when they are put into water (with nothing else). In this case, only one proton (the one with the largest K_a dissociates to any large extent. These can then be treated essentially as weak acids with only one proton. The other protons in compound will generally all be essentially 100% in their protonated state. For example, if you place H₃PO₄ into water, it will dissociate and form H₃O⁺ and H₂PO₄^- to a small extent since the K_a for this first proton is 7.1 x 10^-3. However, in this solution you will have essentially no HPO₄^2- or PO₄^3- as the next two protons are so weakly acidic that they will never dissociate in this solution. The only way to "pull" them off the molecule would be to neutralize the first proton by adding a strong base to the solution.

A special polyprotic acid is sulfuric acid. The first proton has a larger enough equilibrium constant to be considered strong, and the second proton is weak (but with a fairly large Ka). Most of the approximate formulas we developed for acids solutions fail for sulfuric acid for these reasons.

Protonation states of Polyprotic Acids

Just as the protonation state can be determined for a conjugate acid/base pair by comparing the pH to the pKa, the protonation state for each proton in a polyprotic acid can be found making the same comparision.

That is, if you find the compound at a particular pH, how many of the protons are "on" the molecule (in the protonated form) and how many are "off" the molecule (in the deprotonated form)?

For example, consider the polyprotic acid, oxalic acid

This has two carboxylic acid groups (COOH).  This compound could be written as (COOH)₂.  As a consequence, it has two acidic protons.  The pK_a for these two are

pK_a1 = 1.25
pK_a2 = 4.14

Examining the compound in aqueous solutions of different pH, it is possible to determine whether 1 or 2 protons would be "on" or "off" the molecule under different conditions.

First imagine the compound is in a solution that has a pH = 10.  That is rather basic.  The question is, "is pH=10 basic compared to the pKa's of the protons".  This can be determined by comparing the pH and pK_a's.   In this case the pH is more basic than both the pK_a's (pH > pK_a). Therefore both protons will "deprotonated".   The solution would have the majority of the compound in the fully deprotonated form (COO^-)₂.   If instead the solution was very acidic situation pH = 0, then comparing the pH to the pKa's, the solution is more acidic than both the pK_a's (pH < pK_a) and both protons would be "on" the molecule.   The predominate form in solution would be the fully protonated (COOH)₂.   Finally, consider a pH that is between the two pK_a's.   At a pH = 2.5, one proton would be "off" since this is more basic than the first pK_a (that proton would be deprotonated), but it is more acidic than the second pK_a (that proton would be protonated).   The predominate molecular form would be the singly protonated (COO)^-(COOH).

What about other pH values?  What if the pH was equal to pK_a2?  Then we would expect to find the first proton completely off (as the pH is more basic than the first pK_a), but the second proton would be at a pH where we would find it half protonated and half deprotonated.