Introduction to Electrochemistry

Electrochemistry deals with oxidation/reduction reactions.  These reaction are associated with transfer of electrons between chemical species.  For many reactions, we can separate the two halves of the reaction oxidation and reduction and have them take place in physically different locations.  Then, rather than having the electrons transferred directly between the two species, we can force them to flow through an external circuit.

A key idea in electrochemistry is that the electrical potential (voltage) is related to the free energy of the reaction.   This allows us to both measure the free energy as well as control the free energy by applying an external potential.  In this way, we can make non-spontaneous reactions spontaneous by changing the free energy of the reactants and products with an external potential.

Finally, there are many applications of electrochemistry ranging from batteries to fuel cells which convert chemical energy into electrical energy or the opposite process where electrical potential is used to drive chemistry for splitting water into hydrogen and oxygen or making sodium metal from molten sodium chloride.

Introduction to Redox Reactions

Oxidation and reduction are key concepts in electrochemistry.  Chemistry involving oxidation and reduction is typically referred to as Redox chemistry.  Oxidation involves the loss of electrons from a species and reduction involves the gain of electrons.  Because we are never creating new charges out of nothing (aside from nuclear chemistry), we always have oxidation in conjunction with reduction.

Therefore in any Redox reaction, one species is always oxidized and another is reduced.  We can't have one without the other.  Finally, the number of electrons involved in this process must be balanced.  That is, the number of electrons lost by one species needs to be the same as the number gained by the other.  You can't simply build up a beaker full of electrons.

Here are worksheets to practice balancing redox reactions.

• Balancing Redox Reactions
• Balancing Redox Reactions KEY

Oxidation and Reduction

If something is oxidized then its oxidation number goes up.  Oxidation is the loss of electrons.

If something is reduced then its oxidation number goes down.  Reduction is the gain of electrons.

Here are two pictures and ways to help you remember this.  Pick one and remember it forever.

1. LEO says GER Lose Electrons Oxidation.  Gain Electrons Reduction.

2. OIL RIG  Oxidation Is Loss.  Reduction Is Gain.

An Example

Let's look at the following reaction:

\[\rm{2Fe(s) + 3O_2(g) \rightarrow 2Fe_2O_3(s)}\]

In this reaction, the oxidation number of iron starts at zero and then goes to +3.  The oxidation number of oxygen starts at zero and goes to -2.  The iron is oxidized.  The oxygen is reduced.  Note: the name oxidation comes form the fact that reaction with oxygen leads to oxidation.

We can further put "names" on the compounds involved in the Redox reaction to identify their "actions".  In this reaction, we would call oxygen the "oxidizing agent" since it is oxidizing the iron.  The iron would be the "reducing agent" since it is reducing the oxygen.  There is always oxidation with reduction, so we always have an oxidizing agent and a reducing agent.  However, often in reactions we only identify one of them (the other is then identified by default).

Redox Numbers

In order to identify Redox chemistry, chemists have developed a system by which we can think about the "number of electrons" a certain element "has".  This is an idea that simply helps sort out the oxidation and reduction process.

In every chemical species, we can assign an oxidation number (or oxidation state) to each element.  This can be thought of as the number of electrons that "belong" to that element compared to the number of valence electrons the element has.  It is important to note that this is an idea that helps us to think about and classify the chemistry.  Within a compound the electrons don't have any labels and don't belong to anyone one element.  This is merely an accounting trick for us to use as chemists.

Assigning oxidation numbers is very straight forward for atomic ions.  Take Na⁺ as an example.  Normally sodium has one valence electron.  As an ion it has zero valence electrons.  We could then state that the oxidation number (or oxidation state) of Na⁺ is plus one.  It is "missing" one electron.   Similarly the oxidation state of Cl^- is negative one.  It has an "extra" electron.  So for any atomic ion, the oxidation state is simply the charge.  So in the compound NaCl, the oxidation number for Na is +1 and the oxidation number for Cl is -1.

What about polyatomic ions or compounds?   For these we need to consider the oxidation state for each element in the chemical species.  Here the oxidation number can be thought of as the charge that atom would have if the chemical species were broken up.  It is as if we are thinking about all compounds as being ionic compounds.

For this we have a series of rules.

1.  The sum of all the oxidation numbers in a chemical species must equal the charge on the chemical species.  Therefore if we are looking at a neutral molecule, when we add up all the oxidation numbers for all the atoms in the molecule, we should get zero.  If we have a polyatomic ion with a charge of -2, then the sum of the oxidation numbers of all the atoms should be -2.   This is the most important rule.  It will help us figure out the oxidation number of any elements that are not "assigned" a number.

2.  The oxidation number of an atom in its neutral elemental state is zero.   Monatomic species have no charge.  Diatomic species if they break will end up as neutral atoms.  For example, what is the oxidation number of oxygen in O₂?  Zero.

3.  The oxidation number for a monatomic ion is its charge. See above.

4.  Hydrogen is given the oxidation number of +1.  Unless it is bonded to a metal in which case it is -1.  (Note: H₂ is not a compound.)  What is the oxidation state of H in H₂O?  +1.  What is the oxidation state of H in CH₄? +1.  In LiH?  -1.  In H₂.  0.

5.  Oxygen is given the oxidation number of -2.  Unless it is bonded to another in a peroxided bond (oxygen oxygen single bond).  Then it is -1.   What is the oxidation number of O in H₂O?  -2.  In hydrogen peroxide, H₂O₂? -1.

6. The most electronegative element is assigned its charge as an ion.  What is the oxidation state of Mg and Br in MgBr₂?  Br is -1,  Mg is +2.  This is essentially the rule for the monatomic ions.

From there you can work out any element in any compound.  General rule.  Assign H and O first.  The rest typically fall out form there.

What is the oxidation state of N in NH₃?  H is +1, the whole compound is neutral, so N must be -3 since there are three hydrogen at +1 each.

Balancing Redox Reactions

There are many methods to balance redox reactions, but it is best to pick a method and approach it systematically.

Here, one method (the half reaction method) will be presented.  If another methods works better for you, then great.  If not, learn this one and practice it.  An important idea is that balancing Redox reaction is different in acidic versus basic conditions.  This is because the reaction involves either H⁺ or OH^-  which will affect both the elements and the charge.

Here is the half reaction method in acidic solutions.

Step 1: Determine the oxidation numbers of the elements in the reaction and identify the oxidation and reduction reactions.

Step 2: Identify the oxidation and reduction half reactions and write the equations for each.

Step 3: For each half-reaction, balance all elements except for hydrogen and oxygen.  Then balance the oxygen by adding H₂O.  Then balance the hydrogen using H⁺.  Finally balance the charge in the half-reaction using electrons.

Step 4: Multiply one or both of the balanced half-reaction by whole numbers to equalize the number of the electrons in each half-reaction.

Step 5: Double check that all the elements and charge are balanced.

The half reaction method in basic conditions is nearly identical.  The steps are the same up through step 5.

Step 6: We now have a balanced equation except it has H⁺ and we want to get to basic conditions.  So now, add enough OH^- to each side of the equations to neutralize away any H⁺.  One side of the equation should now have the same number of H⁺ and OH^-.  These form water, H₂O molecules.  Now, cancel out any waters that appear on both sides of the equation.

Step 7: Double check that all elements and charge are balanced.

Electrochemical Cells

In an electrochemical cell, we physically separate the oxidation and reduction chemistry in different "compartments".  The electrons from the oxidation are then run through an external circuit before being used in the reduction reaction.   As this is moving negative charge from one location to another, we need to compensate for this by moving other charges to balance this displacement of charge.  This is accomplished by using a salt bridge that allows the migration of spectator ions to balance the flow of electrons.

Each half of the electrochemical cell has an electrode to which the wire for our external circuit is connected.  The chemistry takes place at the surface of this electrode.  The electrode on the oxidation side is called the anode.  The electrode on the reduction side is called the cathode.  As a short hand, we simply refer to the two sides of the cell as the anode side and the cathode side.

For any given set of conditions, the chemistry is spontaneous in only one direction.  When the cell is set up such that this is the direction we desire, we call the cell a voltaic cell (or a galvanic cell or a battery).  When we want the chemistry to go in the non-spontaneous direction, the cell is an electrolytic cell and requires an external power source to drive the chemistry in a non-spontaneous direction.  It is important to note that this is one of the amazing things about electrochemistry.  We can use an external voltage to change the direction of a chemical reaction by adjusting the free energy (we essentially get to chose which is lower in free energy the products or reactants).  So with an electrochemical cell, we can get a chemical reaction to move in both the spontaneous and the non-spontaneous direction.  You are all familiar with this concept but you might not have thought about it as chemistry.  When you are using a battery you are running a voltaic electrochemical cell in the spontaneous direction.  When it gets to equilibrium the voltage on the battery is zero and no more current flows.  However, you can "recharge" the battery by attaching it to an external power supply and forcing the chemistry to go in the reverse direction until you have regenerated the original chemical contents.

For more practice with electrochemical cell problems, see the worksheet and key below.

• Electrochemical Cells_new problem 5
• Electrochemical Cells_new problem 5 KEY

Attachments
• Standard Reduction Potentials at 25 C TABLE

Electrochemical Cell Parts

In an electrochemical cell, we are running a redox reaction, but we have physically separated the oxidation and reduction reactions into different locations.  These take place in different "halves" of the cell.

We then connect the two halves of the cell with an external wire to allow for electron flow from one side to the other.  We also connect the two halves with a "salt bridge" to allow spectator ions to flow to counter balance the electron flow.

The oxidation and reduction reactions are now in different locations.  To allow the electrons to flow from the oxidation reaction (that is producing electrons) to the reduction reaction (that is consuming the electrons), we need to connect the two reactions electrically. This is accomplished by using metal electrodes.  These electrodes serve a the place where the chemistry is taking place.  Sometimes they are part of the reaction.  Sometimes they are simply used as a means to "deliver/collect" the electrons.  The electrode in the oxidation reaction is call the anode.  The electrode for the reduction reaction is called the cathode.  The electrons flow from the anode to the cathode.

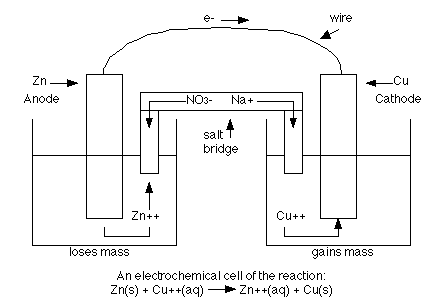
Let's look at a picture of the cell below which contains zinc metal and zinc ions on the oxidation side and copper metal and copper ions on the reduction side.

The left hand side is a picture of the anode half of the cell where the oxidation is taking place.  The solid piece of zinc is the anode.   The righthand side is the reduction half where the copper 2+ ions are being reduced to copper metal.  The solid piece of copper is the cathode.  The two sides are connected by a wire that allows electrons to flow form the anode to the cathode.  They are also connected by a salt bridge.  Since negative charge is flowing from the anode side to the cathode side, some spectator ions need to compensate this flow (or the cathode side will end up with lots of extra negative charge).  So in the salt bridge either sodium + ions could flow from the anode side to the cathode side or sulfate 2- ions could flow from the cathode side to the anode side.  Or both could happen.

For some reactions, neither the reactants nor the products are a metal.  In this case, an inert (non-reactive) metal electrode is required to deliver/collect the electrons for the reaction.

For example, in the cell below at the anode, Fe²⁺ is oxidized to Fe³⁺.  This reaction occurs at the surface of a Pt electrode.

Cell Short Hand

It becomes very cumbersome to draw a picture of an electrochemical cell each time you would like to discuss one.

As such, we have developed a short hand notation for a cell.

For the cell above we have the anode on the left and the cathode on the right.  The oxidation is occurring at the anode

\[\rm{Ni(s) \rightarrow Ni^{2+}(aq) + 2e^-}\]

The reduction is occurring at the cathode

\[\rm{2H^+(aq) + 2e^- \rightarrow H_2(g)}\]

The overall reaction is

\[\rm{Ni(s) + 2H^+(aq) \rightarrow Ni^{2+}(aq) + H_2(g)}\]

Rather than having this picture of the cell, we have a shorthand that is the same moving from left to right in our diagram.  We start with the anode which we write to the right of a "" symbol.  In total, this will look like

< Ni | Ni²⁺ ||  H⁺ | H₂ | Pt >

This is the most generic of notations.  To be more specific we might include the concentrations (or pressures) along with the phases.

< Ni(s) | Ni²⁺ (aq,1M)  ||  H⁺ (aq, 1M)  | H₂ (g, 1 atm) | Pt(s) >

Reading this from left to right, we have a nickel anode that is oxidizing to Ni²⁺ connected by a salt bridge to a solution of H⁺ that is reducing to H₂ gas at a Pt cathode.  Note: on both the anode and cathode sides of the notation the reactants are on the left and the products are on the right. (Ni -> Ni²⁺) (H⁺ -> H₂).  Also, in the cell notation the half reaction might not be balanced with each other or themselves.  For example you write H⁺ not 2H⁺ because if you have a concentration, it is for H⁺.

Standard Hydrogen Electrode

For any half reaction, we can measure the potential (free energy) by comparing it to a standard reaction.  The reaction we choose is the following.

\[\rm{2H^+(aq) + 2e^- \rightarrow H_2(g)}\]

Where the concentration of the H⁺ is 1M and the pressure of the H₂ gas is 1 atm. Such an electrode is called a "standard hydrogen electrode" or SHE.

We can then make a cell with any other half reaction (under standard conditions where concentrations are 1M) and measure the potential (voltage).

For example here is a cell to compare the potential of the reaction of Ni to Ni²⁺ to the SHE.

We can then measure all such combinations and tabulate the data.  Note: for some reactions, we are measuring the oxidation and for others the reduction, but we will always tabulate the reduction potential for the half reaction.

Standard Reduction Potentials

Having compared many reactions to the standard hydrogen potential, we can now make a table of reduction potentials for all half-reaction, (or oxidation potentials but we need to pick one and stick to it).

Below is a table for reduction potentials.

At the top of the table are the reactions that are "easiest" to oxidize and thus the hardest to run as reductions.  At the bottom are the easiest reductions, and thus the most difficult to run as oxidations.

When looking at the table, we need to be careful since everything is written as a reduction. For example, from this table we can find the substance that is easiest to oxidize.  That is from the top of the table.   But the substance that is being oxidized appears as a product in this table.   Li(s) is the easiest to oxidize.  The easiest to reduce is a reactant in the table. F₂ gas is the easiest to reduce.

Since Li is easy to oxidize, it is an excellent reducing agent (it reduces something else when it is oxidized).   F₂ is a great oxidizing agent (it oxidizes something else when it is reduced).

From this table, we can now figure out what reactions will be spontaneous.  For example, if something is higher in the table (lower potential) it will be oxidized while the reactions with higher (more positive potentials) will be reduced.

Will Ag⁺ oxidize Fe?   Yes.  How do we know? The reduction potential for Ag⁺ is more positive than that for Fe²⁺.  So Ag⁺ is a strong enough oxidizing agent to oxidize Fe to Fe²⁺. On the other hand it could not oxidize H₂O to H⁺ and O₂.

Below is as more extensive table of standard reduction potentials.  An even larger data set can be found on the wikipedia link below. A pdf document of the Standard Reduction Potential Table used in class can be found on the attachment below.

Attachments
• Standard Reduction Potentials at 25 C TABLE

External Resources
• http://en.wikipedia.org/w … ode_potential_(data_page) -

Standard Cell Potentials

We can calculate the standard potential for any electrochemical cell from the standard potentials of the two half reactions.

For example, imagine we had the following cell.

< Ni | Ni²⁺ || Fe³⁺ , Fe²⁺ | Pt >

We have at the anode side the reaction

\[\rm{Ni \rightarrow Ni^{2+} + 2e^-}\]

and at the cathode side the reaction

\[\rm{Fe^{3+} + 1 e^- \rightarrow Fe^{2+}}\]

The standard potential for this cell is simply

\[\rm{\mathcal{E}^{\circ} = \mathcal{E}^{\circ}_{cathode} - \mathcal{E}^{\circ}_{anode}}\]

Where \(\mathcal{E}^{\circ}\) for each electrode is the standard reduction potential for the half-reaction.  Using our table of standard reduction potentials we find for

\[\rm{Ni^{2+} + 2e^- \rightarrow Ni(s) \mathcal{E}^{\circ} = -0.25 V}\]

\[\rm{Fe^{3+} + e^- \rightarrow Fe^{2+} \mathcal{E}^{\circ} = +0.77 V}\]

So the standard potential is

\[\rm{\mathcal{E}^{\circ} = \mathcal{E}^{\circ}_{cathode} - \mathcal{E}^{\circ}_{anode} = 0.77 - (-0.25) = +1.02 V }\]

VERY IMPORTANT.  Note: the potential is simply the energy difference between the two half reactions.  Do not try to multiple the potentials by the number of electrons.  The number of electrons simply relates how many electrons there are per reaction.  How many Fe³⁺ will be reduced per Ni atom that is oxidized.  The potential difference (free energy difference) between the two half-reactions is not dependent on the number of electrons.

Voltaic Cells

An electrochemical cell in which the chemistry is spontaneous is called a voltaic cell.  This means that the oxidation will occur spontaneously at the anode and the reduction spontaneously at the cathode.  We should note that the notation of something as a voltaic cell is a choice.  Just as we choose what we want to call the "reactants" and "products" in a chemical reaction, our choice of anode and cathode is based upon what chemistry we would like to see occur.  For a voltaic cell our choice ends up being the spontaneous choice.

The standard potential for a voltaic cell is positive.  The standard free energy for a reaction Δ_rG⁰ is related to the standard potential, E⁰, such that negative free energy (spontaneous) corresponds to positive potential.  The beauty of electrochemistry and electrochemical cells is that we can now directly measure the free energy difference by measuring electrical potential.

Voltaic cells can be referred to as Galvanic Cells.  This is a different word for the identical concept.  They are also batteries.  Since a battery is an electrochemical cell that produces a voltage (and current) spontaneously, it is a voltaic cell.  You will find these three terms used interchangeably.

Below is a picture that summarize the ideas for a voltaic cell.

For a voltaic cell E > 0,  ΔG < 0.
Electrons flow from anode to cathode.
The one odd detail is the "sign" of the electrodes.  For a voltaic cell the cathode is assigned the "+" sign.

Electrolytic Cells

An electrochemical cell in which the chemistry is non-spontaneous is called a electrolytic cell.  This means that the oxidation will not occur spontaneously at the anode and the reduction will not be spontaneous at the cathode.  This means we would like chemistry to occur that is uphill in free energy.  This means that it can't happen unless we make it happen.  For most chemical reactions, this can only be accomplished by coupling it to another reaction in which the free energy change is sufficiently negative that the two reactions together are spontaneous.  In the case of electrochemistry, it is significantly easier as we can simply drive the reaction by attaching an external power supply.

The standard potential for a voltaic cell is negative.  The standard free energy for a reaction Δ_rG⁰ is related to the standard potential, E⁰, such that positive free energy (non-spontaneous) corresponds to negative potential.  To make the reaction "go," we must apply a voltage that is significant enough to overcome the negative potential of the cell itself.

Electrolytic cells thankfully don't have many names.  However processes such as electroplating, or electrodeposition are typically electrolytic cells.

Below is a picture that summarizes the cell nomenclature for a electrolytic cell.

For an electrolytic cell E < 0,  ΔG > 0.
Electrons flow from anode to cathode (this is always the case). For an electrolytic cell however, this flow is not spontaneous but must be driven by an external power source.
In an electrolytic cell, the anode has the "+" sign.

Electrochemistry and Stoichiometry

Charge and Current

In electrochemistry, we are often interested in the number of electrons that have flowed through our cell.  This is then related to the mass of the reactants consumed or products formed.  However, we generally don't measure charge in the lab.  Instead, we measure current.

\[\rm{current = {charge \over time}}\]

Current is the amount of electrical charge that flows during a period of time. Typically we measure this in units of Amperes or Amps.  Where 1 Amp (A) = 1 Coulomb (C) per second (s)

\[\rm{Ampere = A = {Coulomb \over second}={C \over s} }\]

We can rearrange this relationship to find the time it takes to get a certain charge with a particular current or the total charge from a current flowing for a given time.  Or we could use the charge and time to calculate the current.  You should be able to manipulate this in any way given two of the variables to find the third.

Faraday's Constant

In keeping track of how much chemistry is taking place in an electrochemical cell, we have a great advantage since we can direct and measure the amount of current that flows through the cell (thanks to the wonders of electrical measurement).

So we need a means by which we can convert charge to numbers of electrons.

For this we use Faraday's Constant.  Faraday's Constant is given the symbol \(\mathcal{F}\) and is defined as the charge in Coulumbs (C) of 1 mole of electrons.   Faraday's constant is approximately 96,485 C.  You can calculate \(\mathcal{F}\) by multiply the charge on one electron (1.602 x 10^-19) by Avogadro's number (6.02 x 10²³).

So imagine we have the following electrochemical cell

< Zn | Zn²⁺ || Ag⁺ | Ag >

How much charge will flow through the cell if 5 g of Zinc react?   For this we need the balanced electrochemical equation.  For the potentials, all we needed was to identify the half-reactions.  For stoichiometry we need a balanced equation. For this cell, the balanced equation is

\[\rm{Zn(s) + 2Ag^{+} \rightarrow  Zn^{2+} + 2Ag(s)}\]

In addition, we need to realize that the number of electrons that are flowing per zinc is 2.  We can figure this out using oxidation numbers.  Zn is going from 0 to a 2+ oxidation state.  This is most obvious if you write out the two balanced half-reactions

\[\rm{Zn(s) \rightarrow Zn^{2+} + 2e^-}\]

\[\rm{[ {Ag^{+} + e^- \rightarrow Ag(s)}] \times 2}\]

For this reaction, we would say the number of electrons, n, is two.  For every zinc atom that reacts, it produces two moles of electrons.  For every mole of electrons we have  \(\mathcal{F}\) coulombs of charge.

Current and Voltaic Cells

For a voltaic cell, the chemistry is spontaneous.  Therefore once the cell is connected the chemistry drives electrical current through the external circuit.

The amount of chemistry can be quantified by measuring the current over time.  Typically, the current might change over long periods of time, but for short periods, it would likely be constant.  Therefore we can relate the current and time to the total charge that has passed between the anode and the cathode.  Knowing the charge, we can figure out how many moles of electrons there were.  Knowing how many electrons will tell us about how many moles of  reactants have been consumed and how many moles of product are formed.

In a typical alkaline battery the half-reactions are

\[\rm{Zn(s) + 2OH^-(aq) \rightarrow ZnO(s) + H_2O(l) + 2e^-}\]

\[\rm{2MnO_2(s) + H_2O(l) + 2e^- \rightarrow Mn_2O_3(s) + 2OH^-(aq)}\]

Note: the batteries are called alkaline because they have a basic pH not because they use alkali metals.   Also, the liquid water and hydroxide are not really a "liquid solution" as they are typically in a more solid suspension.

Assuming you had such a battery and used it to power your wireless mouse.  This device might draw 1 mA of current (I think personally that is a bit high, but maybe you are really active with you computer mouse).  You can run a typical AA battery at this current level for 2000 hours.   If you ran you battery at a constant 1 mA for 2000 hours, how many grams of Zn would be consumed?

Well first, we need to convert current to charge.  Current is charge per time.  So charge is current multiplied by time.   2000 hours = 120,000 seconds.  1 mA = 10^-3 A.  So the total charge is  (10^-3 C s^-1)(120,000 s) = 120 C.

How many electrons is this?  We need to use Faraday's constant.

Moles of electrons = 120 C / 96,485 C mol^-1 = 1.24 x 10^-3 moles of electrons.

Looking at our oxidation half reaction, we see that for every mole of zinc there are two moles of electrons.  So the moles of Zn = moles of electrons/ 2 = 1.24 x 10^-3/2 = 6.2 x 10^-4 moles of Zn.  The grams of Zn is then just this number of moles times the atomic mass of Zn.  Grams of Zn = 6.2 x 10^-4 mol x  65.4 g mol^-1 = 0.04 g

Current and Electrolytic Cells

There is no difference in working stoichiometry problems for electrolytic cells vs voltaic cells.  It is simply a conversion between current, time, and charge and using Faraday's constant to convert between charge and numbers of moles.

Below is a video of a worked example.

Electrochemistry and Free Energy

The most amazing thing about electrochemical cells is that by separating the oxidation and reduction reaction into different compartments, we now have the ability to directly measure the free energy of the reaction by measuring the electrical potential.

The potential or voltage or EMF or whatever you prefer to call it is a measure of the free energy of the reaction.  This is because the difference in free energy between the reactant and the products directly corresponds to the electrical potential of the cell.

Free Energy and Work

When looking at chemical reactions, we often talked about the difference in free energy between the reactants and products.  This was either Δ_RG at whatever conditions existed currently or if it was given at standard conditions, we had Δ_RG °.

Previously, we discussed this in terms only of spontaneity.  However, Δ_RG has another interpretation.  It corresponds to the maximum reversible work we can extract from this chemical reaction.  While previously you may have dealt with the concept of "work" in the context of pressure-volume work, the "work" we are interested in now is electrical work.

Electrical work is defined as charge times potential.   This will give us an energy.  The total work would be the charge that is run through the cell times the potential of the cell.  For a reaction, we are typically interested in the work (or energy) per mole of reaction.  This is how we defined Δ_RG with units of kJ mol^-1.  Looking at this, we get

\[\rm{work = \Delta G = -n \mathcal{FE}}\]

Here ΔG is not for the standard conditions, but for the conditions now.  So the potential E is not the standard potential but the potential now.  n is the number of electrons per mole reaction as the equation is written.  F converts between mole of electrons and charge in coulombs.  Note: the energy you get is still per mole, but it is per mole reaction (not per mole of electrons).

With this relation, we can now convert directly between differences in free energy and differences in electrical potential!

Standard Potentials and K

Since we can relate free energy differences and electrical potentials at any conditions, then we can relate them at standard conditions.

\[\rm{\Delta _R G^{\circ} = -n\mathcal{FE}^{\circ}}\]

Since Δ_RG° is related to the equilibrium constant K, we can now relate K and E°!

\[\rm{\Delta _R G^{\circ} = -RTlnK}\]

\[\rm{\mathcal{E}^{\circ} = {RT \over n \mathcal{F}}lnK}\]

Assuming a temperature of 298K and converting from ln to log₁₀ we get

\[\rm{\mathcal{E}^{\circ} = {0.059 \over n}logK}\]

As such Δ_RG° , K , and E° are all different ways to state the same concept.

Δ_RG° < 0  is K > 1 is E° > 0 is "spontaneous" and favors the products

Δ_RG° > 0  is K < 1 is E° < 0 is "non-spontaneous" and favors the reactants

Nernst Equation

What if I'm not at standard conditions?

Imagine you have a voltaic cell at standard conditions to start.  Now, you let the chemistry start by wiring up the cell and allowing the electrons to flow from anode to cathode.  As the chemistry proceeds, the concentrations are changing and the potential is changing.  The reaction will "go" until the system reaches equilibrium.  At this point, the potential will be zero.  Clearly the potential must change as the concentrations are changing.  How can we determine the potential under any concentration conditions not just standard conditions?

We can use our free energy relations.  Before, we could figure out if a reaction was at equilibrium by comparing the ratios of the concentrations "now" to what they would be at equilibrium.  This was a comparison between the mass action expression now "Q" and what it is at equilibrium "K".   Thinking back to free energy and equilibrium we can remember that

\[\rm{\Delta _RG = \Delta _RG^{\circ} +RTlnQ}\]

If we put in our relationships for ΔG and E we get

\[\rm{\mathcal{E} = \mathcal{E}^{\circ} - {RT \over n\mathcal{F}}lnQ}\]

The last term can be converted to a simpler form by inserting in all the constants (assuming 298K) and converting form the natural log to log base 10.

\[\rm{\mathcal{E} = \mathcal{E}^{\circ} - {0.0591 \over n}logQ}\]

This equation is called the Nernst equation.

Calculating a potential

The Nernst equation can be used to calculate the potential of an electrochemical cell under any conditions.  Let's look at an example of this using the very simply cell

\[\rm{< Zn(s) | Zn^{2+}(aq) || Cu^{2+}(aq) | Cu(s) > }\]

The balanced equation for this cell is

\[\rm{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)}\]

For this reaction, we can look up the standard half reduction potentials and calculate the standard potential E°.  In this case, you find that E° = 1.1 V.

Now the question is, what is the potential under other conditions.  For this let's look at an example where we [Zn²⁺] = 0.1 M and [Cu²⁺] = 0.001 M.

To find the potential, we need to use the Nernst equation

\[\rm{E = E^{\circ} - { 0.059  \over n}logQ}\]

Here n=2 since the equation as written has 2 electrons per mole reaction.  Now we need Q.

\[\rm{Q = {[Zn^{2+}] \over [Cu^{2+}]} = {0.1 \over 0.001} = 100}\]

Plugging this into the Nerst Equation with the standard potential, we get

\[\rm{E = 1.1 - { 0.059  \over 2}log(100) = 1.1 - 0.029(2) = 1.04 }\]

Since the conditions are closer to equilibrium than the standard conditions the potential is lower.

You should be able to manipulate the Nernst equation in any way.  Given a potential and standard potential, you should be able to determine ratios of concentrations or an unknown concentration.   Given concentration and standard potential, you should be able to find the potential, etc...

© 2013 mccord/vandenbout/labrake

scroll to top