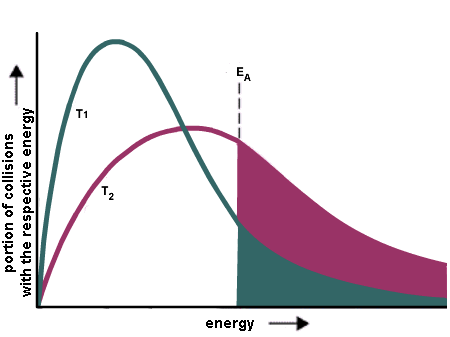
The rate of a reaction depends on the height of the barrier (the activation energy) because only a small fraction of the number of molecules at a given temperature have sufficient energy to get over the barrier. At a given temperature, there is a distribution of kinetic energies for all the molecules in a sample (this is the Boltzmann distribution). This molecular kinetic energy can describe things like vibrations of molecules even for samples like solids that might not be "moving".
This distribution has a long tail to high energy. So there are always a few molecules with sufficient energy to get over the barrier (energies greater than Ea). As the temperature is raised, the distribution shifts to higher energy and so more molecules have sufficient energy to get over the barrier.
This can be quantified using the Boltzmann distribution such that we can write down an expression for the rate constant as a function of temperature
\[k = A \exp\left({-E_a \over RT}\right)\]
Where k is the rate constant, Ea is the activation energy, R is the gas constant, A is a constant called the pre-exponential factor, and T is the temperature. This formula is essentially a comparison between the energy of the molecules (RT) and the energy of the barrier (Ea). The pre-exponential factor is a constant that is specific to the reaction and it is essentially the ultimate rate of the reaction. This is the fastest the reaction could ever proceed (if the barrier were zero or the temperature were infinite).
This leads to a very general conclusion. A barrier exists for most all chemical reactions. Therefore as the temperature increases, the rate of all reactions increase. This has little to do with the molecules moving faster and colliding more often. It has everything to do with the molecules having more energy and making it over the barrier along the reaction coordinate.
Raise the temperature and the reaction will go faster. Why? The rate constant is larger at higher temperatures.
The Arrhenius equation is often used to compare the rate constants measured at two different temperatures. Using two sets of data points, the equation can be rearranged to yield
\[\ln \left({k_2 \over k_1} \right) = {-E_a \over R} \left({1 \over T_2} - {1 \over T_1} \right)\]
or
\[\ln \left({k_2 \over k_1} \right) = {E_a \over R} \left({1 \over T_1} - {1 \over T_2} \right)\]
This equation can also be written as
\[\ln k = \ln A - {E_a \over RT}\]
Therefore if one measures rate constants at many temperatures and constructs a plot of lnk vs 1/T the slope of the plot will be -Ea/R and the intercept will be lnA.
Arrhenius Law© 2013 mccord/vandenbout/labrake