Nuclear change is distinct from chemical change in that elements change. Chemical change is all about the electrons. In chemical change, the nuclei are conserved and simply change how they are bonded together(the electrons). In nuclear change, it is all about the nuclei. In a nuclear change the elements can change from one to another. Nuclei can break apart to form smaller elements. Nuclei can fuse together to make heavier elements. Neutrons can turn into protons and protons into neutrons. For nuclear change we essentially ignore the electrons completely. We are occasionally interested in high energy electrons that are emitted as "radiation", but otherwise we simply ignore the electrons as if they are not part of the atom at all. This is because the changes in energy related to the nuclei are so larger, we can simply focus on the nuclear part of the changes.

Nuclear vs Chemical Change

For a nuclear change (reaction) we no longer have a "conservation of atoms". We can balance a chemical reaction by making sure that we have the same number of each type of atom on each side of the reaction. This is not the case at all in a nuclear reaction since the number and type of atoms can both be changing.

However, we can still balance a nuclear reaction. To balance a nuclear reaction, we need to make sure that both sides of the reaction have the same charge and the same mass number. The mass number is simply the total number of protons and neutrons (taking each as mass number 1). This is an estimate of the total mass of the nucleus. However, while the mass number is conserved the mass is not. This is because the energy associated with a nuclear change is so large that the change in mass is detectable. Whenever there is an energy change we have a mass change, but for chemical reactions this mass change is so small we don't worry about it. For nuclear change, the energy is so large that the small change in mass becomes detectable.

As such, a key distinction between nuclear vs chemical change is the energy. The change in energy for a chemical reaction has to do with the potential energy of the electrons. The change in energy for a nuclear reaction has to do with the potential energy of the nucleus. The change in energy for a nuclear change is many orders of magnitude larger than for a chemical change. A typical chemical reaction might be a few hundred kilojoules per mole. A typical nuclear reaction might be 10 billion kilojoules per mole. That's billion with a "B".

Mass and Charge Number

To keep track of mass and charge in a nuclear change (reaction), we need to understand the notation that is utilized. The first thing to realize is that unlike chemistry where we look at atoms (nuclei + electrons), nuclear change often only looks at the nuclei and ignores the electrons.

Because the reactions deal with the nuclei, we need to know which specific isotopes we are dealing with for each element. Therefore we are always looking at specific isotopes (numbers of protons and neutrons) for any element rather than some natural mixture of isotopes.

First, a definition. nuclide: an atomic species specified by its number of protons and neutrons.

For example, a nuclide could be a Helium nucleus that has 2 protons and 2 neutrons. This nuclide would have a mass number of 4 (2 protons + 2 neutron = 4) and a charge of +2. This would be given the following symbol

For a nuclide, the charge is simply the number of protons. This is what defines what element it is. Any species with only two protons is "Helium". That is what makes helium helium. So in our symbolic representation the elements symbol and the charge number are redundant. However, it is very handy since generally it's hard to remember off the top of your head how many protons are in every element.

Any given element could have a large number of different isotopes. Generally they are referred to by their mass number and the element name (which is the charge number). So for example, we could have

This would be called "gold-197". It is gold (Au) since it has 79 protons (the charge number of 79) and it has 118 neutrons (197 - 79 = 118).

Concept Question

How many neutrons does \(\rm ^{133}_{\;53}I\) have?
(mouse over choices to get answer)

80
53
133
none

Nuclear Particles

In addition to nuclides, a nuclear reaction might involve sub-atomic particles.

There are many such particles. For "nuclear chemistry" we are dealing only with the "larger" particles. That is the protons, neutrons, electrons.... As we are not concerned with details of conservation of momentum or spin, we won't worry about other particles such as neutrinos.

Given this we have to essentially deal with four particles

protons (mass number 1, charge 1) \(\rm ^1_1p\)

neutrons (mass number 1, charge 0) \(\rm ^1_0n\)

electrons (mass number 0, charge -1) \(\rm ^{\;0}_{-1}e\)

positrons (mass number 0, charge +1) \(\rm ^0_1e\)

Note: The electrons and positrons have another name. They can be called "beta particles." As such they are sometimes denoted by a beta (+/-) rather than given the symbol "e".

To avoid confusion, one should explicitly state whether the beta particle is + or -. However, the beta particle was discovered in 1900 by Henri Becquerel and was characterized as being the same as an electron. Therefore the term "beta particle" will always refer to electrons in this context and without any other reference point. The positron wasn't discovered until 1932 and it's properties were "opposite" of an electron. So the "positive" electron was born and it was given the symbol \(\beta ^+\). The + sign must be explicitly stated to mean a positron. So, when no sign is given, \(\beta \)-particles are electrons. Only when the sign is given with a +, is it a positron.

Balancing Nuclear Change

If we want to balance a nuclear change (reaction), we need to make sure that both sides of our reaction (reactants and products) have the same mass number and charge number. Just as with chemical change, it can be difficult to predict the products with only the reactants (since many possible changes could occur). Thus, for a nuclear change, typically we are balancing one of many possible reactions. The key is to determine what the missing parameters are.

For example, this is an important fusion reaction (light elements make heavier elements). It is the reaction of two hydrogen atoms to make a helium atom.

\[\rm{^2_1H \;+\; ^3_1H \;\;\longrightarrow\;\; ^4_2He \;+\; ^1_0n}\]

In this reaction, you have three nuclides (two hydrogen nuclei and one helium) and one nucleon (or nuclear particle). This is a bare neutron. The neutron has a mass number of 1 and a charge of 0. You can see the sum of the mass numbers on the right and left-hand side is the same (five on each side) and the sum of the charge is the same (two on each side).

We can look at other changes that are missing something and deduce from the other parts of the change what is missing. For example, let's look at the following reaction which is a fission product (heavier elements make lighter elements) of uranium.

\[{\rm ^{235}_{92}U \;\;+ \;\;^1_0n \; \longrightarrow \;\;^{137}_{56}Ba \;\;+ \;\;? \;\;+\;\; 2 ^1_0n}\]

If we total the mass number of the lefthand side, we see that it is 236. The charge on the left is 92. Therefore we need the same on the right. Without the mystery nuclide we have a mass number of 139 (137 + 2) (note: there are two neutrons so you have to count them both). The charge number is 56. Now we can figure out what is "missing". We need something with a charge of 36 (92-56) and a mass number of 97 (236-139). That is Krypton-97. Krypton because it needs a charge of 36 and mass number 97 isotope since we need that mass.

\[\rm{^{235}_{92}U \;\;+ \;\; ^1_0n \longrightarrow \;\; ^{137}_{56}Ba \;\; + \;\; ^{97}_{36}Kr\;\; + \;\; 2 ^1_0n}\]

Concept Question

What is the missing product in the following reaction?

\[{\rm ^{238}_{92}U \;\; \rightarrow \;\; ? + \;\; ^4_2He}\]

(mouse over choices to get answer)

\({\rm ^{234}_{92}U}\)
\({\rm ^{234}_{90}U}\)
\({\rm ^{232}_{90}U}\)
\({\rm ^{234}_{90}Th}\)
\({\rm ^{238}_{90}Th}\)

Nuclear Reactions

We can classify nuclear changes as a number of different types of nuclear reactions. Each has its own characteristics (and potential applications). In addition, like chemical reactions we can write down an infinite number of nuclear changes that could occur by simply constructing a balanced equation. However, we will focus on typical changes that occur in a number of nuclear chemistry applications. Rather than focus on predicting the outcomes of nuclear change, the goal will be to identify different types of reactions.

The four main reaction types that will be covered in this unit are:

Fission
Fusion
Nuclear Decay
Transmutation

Fission

We can classify a number of nuclear reactions. The first important reactions are fission reactions. In fission reactions, a heavy nucleus is "split" into two (or more) smaller nuclei. Generally, we discuss reactions which are downhill in energy (exothermic). Fission reactions are exothermic that start with nuclei that are heavier than iron.

An example of an important fission reaction is

\[{\rm ^{235}_{\;92}U \;\;+\;\; ^1_0n \;\;\rightarrow ^{137}_{\;56}Ba \;\;+ \;\;^{97}_{36}Kr\;\; + \;\;2 ^1_0n}\]

This is the fission of uranium-235 to make barium-137 and krypton-97 plus a couple of neutrons. Note: there are neutrons on both sides of this reaction. It is important to show them both in the reaction since the neutron instigates the reaction. The fission is actually a uranium-236 nucleus that is created from the collision of a neutron and a uranium-235.

Fission reactions are widely used to generate electrical power using uranium as a fuel and generating a wide array of fission products.

Fusion

Fusion reactions is when two (or more) lighter nuclei come together to make a heavy nucleus. For example

\[{\rm ^2_1H \;\;+\;\; ^3_1H \;\;\rightarrow \;\;^4_2He \;\;+\;\; ^1_0n}\]

The fusion of four hydrogen atoms and two electrons into a single helium atom is the primary reaction in the sun (although it happens in a number of steps). Fusion reactions are exothermic for nuclei smaller than iron.

Fusion reactions of light elements can be extremely exothermic. And per mass generate by far the most energy. Research is on going to maintain stable fusion reactions on earth. Currently, reactions can be maintained for infinitesimally short times (or in uncontrolled reactions such as the hydrogen bomb).

Nuclear Decay

Nuclear decay is perhaps the most important process to understand in nuclear chemistry. This is the origin of "radioactivity" and is the basis of most applications of nuclear chemistry outside of the nuclear power industry. Nuclear decay is the process by which an unstable isotope of a particular element spontaneously transforms into a new element by emission of ionizing radiation. Later the details of the types of such decays as well as the types of radiation will be covered. In many ways, nuclear decay is similar to fission. The product elements are lighter than the reactant elements. However, unlike fission nuclear decay involves one element transforming into another rather than breaking up into two nuclei. Some nuclear decay involves the emission of a He-4 nucleus. Typically this is considered emission of a "particle" versus the nucleus breaking up into smaller pieces. Nuclear decay almost always involves large energy release in the form of radiation. An example is the electron capture reaction below that issued in the treatment of prostate cancer since the decay results in the emission of high energy gamma rays

\[{\rm ^{103}_{\;46}Pd \;\;+ \;\; ^{\phantom{-}0}_{-1}e \;\; \rightarrow \;\;^{103}_{\;45}Rh \;\;+ \;\;\gamma}\]

Transmutation

Transmutation is essentially the reverse of nuclear decay. It is a non-spontaneous process where by one element is converted to another by the bombarding it with high energy radiation (or neutrons). This is generally an artificial process that allows the creation of radioactive isotopes. For example, the Pd-103 that is uses in the treatment of prostate cancer is made in laboratory is made by bombarding Pd-102 with high energy neutrons.

\[{\rm ^{102}_{\;46}Pd \;\;+ \;\; ^1_0n \;\; \rightarrow \;\;^{103}_{\;46}Pd}\]

Transmutation involves increasing the mass of nuclei.

Concept Question

The following is what type of reaction?
\[{\rm ^{252}_{\;98}Cf \;\; \rightarrow \;\; ^{140}_{\;54}Xe + \;\;^{108}_{\;44}Ru \;\;+ \;\;4^1_0n}\]

nuclear decay
transmutation
fission
fusion

Energy and Nuclear Change

Nuclear changes are either endothermic (up-hill in energy) or exothermic (down-hill in energy) just like chemical changes. The difference is that the magnitude of the energy changes are typically much much larger for nuclear changes on a per mole basis. The reason for the change in energy is the change in the potential energy of the nuclei in the reaction.

The potential energy of a nucleus is simply the energy of the nucleus compared to the energy of the sub-atomic parts of the nucleus broken apart. For example, a helium-4 nucleus is comprised of two protons and two neutrons. The helium nucleus is more stable with the four particles in close proximity (all in the nucleus together) than as two separate neutrons and two separate protons. If this was not the case, then helium nuclei would spontaneously break apart into their component parts. The energy difference between the parts and the whole is called the binding energy. The forces that "hold" the nucleus together are of interest only for sub-atomic particles and are not the forces that we are typically familiar with in chemistry. Electrostatic (Coulomb's law) would suggest that the potential energy of a He-4 nucleus would be higher than that of the separated particle since the positive protons should repel each other. This is true at long distances, but at very short distances the nuclear strong force becomes dominate. The potential energy of the protons and neutrons at extremely small distances becomes much lower. Thus the nucleus is more stable than the separated particles (for some combinations of protons and neutrons). This energy that "holds" the nucleus together is the binding energy. A different way to think about the binding energy is that it is the amount of energy needed to break up the nucleus into its parts.

\[\rm{^4_2He \rightarrow 2^1_1p + 2^1_0n}\]

The amount of energy required for this "reaction" is the binding energy of the He-4 nucleus. Conversely if we form a helium-4 nucleus from two protons and 2 neutrons this would be the amount of energy that would be released. The difference in mass between the separate particles and the nuclide is called the mass defect. This "missing mass" is in fact the binding energy.

In the same way that in a chemical reaction some bonds are lower in energy than others (more stable) some nuclei are lower in energy than others. The potential energy of the nuclei is related to nuclear strong force and the nuclear weak force. This a topic that is not explored in detail. However, the key idea is simply that some combinations of protons and neutrons have a lower potential energy (more stable) than others. This is exactly the same as some combination of atoms (bonds) being lower in energy than others in a chemical change.

Take for example the following reaction

\[{\rm 2H_2(g) + O_2(g) \rightarrow 2H_2O(g)}\]

This reaction is exothermic, ΔH_r° = -484 kJ mol^-. That is two water molecules are lower in energy than two hydrogen molecules and one oxygen molecule. Why? The potential energy of the atoms in the water molecules is lower than the atoms in the hydrogen and oxygen molecules. We can calculate this change by calculating the energy required to break the bonds in the reactants and the energy that is gained by forming the bonds in the products. First, all the reactants are broken apart into atoms. Then these atoms are recombined to form the products. This is simply the bond energies of the reactants minus the bond energy of the products.

\[{\rm 2H_2(g) + O_2(g) \xrightarrow{BE_{reactants}} 4H(g) + 2O(g) \xrightarrow{-BE_{products}} 2H_2O(g)}\]

These bond energies could be estimated from bond enthalpy tables or calculated rigorously with quantum mechanics. Finally, this change could be measured in the lab by measuring the enthalpy of the reaction.

This same idea can be applied to nuclear reactions. The difference in energy in the products and reactants is simply the difference in the potential energy of the products compared to the reactants. Take for example the following fission reaction

\[{\rm ^{235}_{92}U + ^1_0n \rightarrow ^{137}_{56}Ba + ^{97}_{36}Kr + 2 ^1_0n}\]

This reaction is extremely exothermic (~10¹³ J mol^-1). This reflects a difference in binding energy of the products compared to the reactants. The combination of Ba-137 and K-97 is more stable than U-235. The transition can be imagined as first breaking up the nuclei into their component parts and then forming the products from the individual protons and neutrons. This the binding energies of the reactants minus the binding energies of the products.

\[{\rm ^{235}_{92}U + ^1_0n \xrightarrow{BE_{reactants}} 92^{1}_{1}p + 144 ^{1}_{0}n \xrightarrow{BE_{products}} ^{137}_{56}Ba + ^{97}_{36}Kr + 2 ^1_0n}\]

Where now BE is the "binding energy" rather than the "bond energy". The binding energy of the two nuclei combined in the products is lower in energy than the one nucleus in the reactants. Thus this reaction releases a large amount of energy.

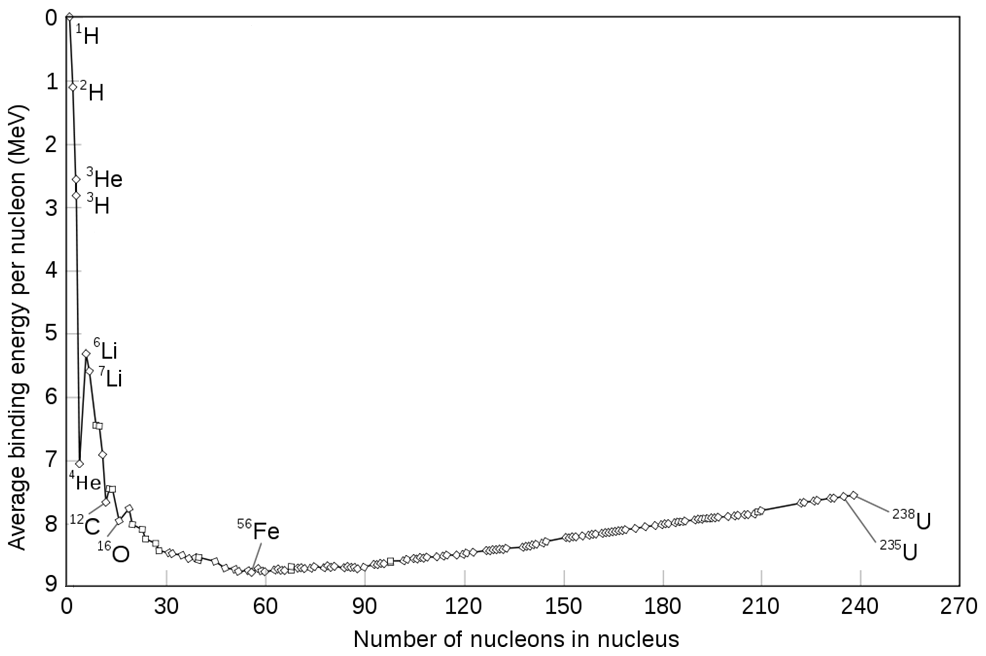
If we were simply to compare the binding energy of nuclei to each other, the largest nuclei would have the highest binding energy since they contain the largest number of protons and neutrons. However, what is of interest is not the total binding energy, but instead the binding energy per nucleon (proton/neutron). The binding energy of nuclei has a particular trend such that the nucleus with the highest binding energy per nucleon (neutron/proton) is iron. Another way to say this is that the most stable (lowest energy) nucleus is iron. Therefore it is downhill in energy for small nuclei to combine to form heavier nuclei if they are lighter than iron. Conversely, it is downhill in energy for larger nuclei to break apart into smaller nuclei for elements heavier than iron. This means that fusion is exothermic for elements lighter than iron, but fission is exothermic for elements heavier than iron. The graph below shows the binding energy per nucleon vs nucleon number (mass number).

Mass and Energy

All of the energy changes in nuclear chemistry can also be described as mass changes since energy and mass are related by the theory of relativity.

\[\Delta E = \Delta m c^2\]

The change in the energy is related to the change in mass times the speed of light squared. This is true not simply for nuclear chemistry but for all energy changes. However, typically the mass changes associated with chemical changes (or other energy changes) are so small that they cannot be quantified. The energy changes in nuclear changes are possible to quantify as the energy changes are so large. This allows us to characterize (measure) energy changes as mass changes.

For a nuclear change then, we need to know the masses of the particular nuclides in the reaction. This not the average atomic mass form the periodic table. We need a very specific table that lists nuclide masses. Then we can look at the mass of the products minus the mass of the reactants. If the mass of the products is less than the mass of the reactants, the "missing" mass has been "converted" to energy. For example, take the binding energy of He-4.

\[\rm{^4_2He + energy \rightarrow 2^1_1p + 2^1_0n}\]

The mass of a He-4 nucleus is 4.0015 u (atomic mass units). 1 atomic mass unit is 1.66054 x 10^-27 kg. The mass of 2 protons + 2 neutrons is 4.0319 u (2 × 1.00728 + 2 × 1.00866). This gives a mass difference of 0.0304 u. This difference in the mass is called the mass defect. This is the mass that is apparently missing in the nucleus when it forms from the nucleons. This mass can be converted to an energy

\[\Delta E = \Delta m c^2 = {\rm(0.0304\;u)(1.66054\times 10^{-27} \;kg)(3.0 \times 10^8 m\,s^{-1})^2 = 4.5 \times 10^{-12}\;J} \]

This gives the binding energy of a single nucleus. Binding energies are often given in keV (kilo-electron volt). 1 J = 6.24 × 10¹⁸ eV. So the binding energy of He-4 nucleus is (4.5 × 10^-12J)(6.24 × 10¹⁸ eV J^-1) = 2.8 × 10⁷ eV or 2.8 × 10⁴ keV.

Similar calculations are possible for any reaction if one knows the masses of all of the reactants and products to sufficient accuracy. The only thing to watch out for is units. Mass is often in grams (not kilograms) per mole. You want all the units in kilograms, meters, and seconds. Then the energy will be in Joules.

Example Mass to Energy Calculations