Nuclear changes are either endothermic (up-hill in energy) or exothermic (down-hill in energy) just like chemical changes. The difference is that the magnitude of the energy changes are typically much much larger for nuclear changes on a per mole basis. The reason for the change in energy is the change in the potential energy of the nuclei in the reaction.
The potential energy of a nucleus is simply the energy of the nucleus compared to the energy of the sub-atomic parts of the nucleus broken apart. For example, a helium-4 nucleus is comprised of two protons and two neutrons. The helium nucleus is more stable with the four particles in close proximity (all in the nucleus together) than as two separate neutrons and two separate protons. If this was not the case, then helium nuclei would spontaneously break apart into their component parts. The energy difference between the parts and the whole is called the binding energy. The forces that "hold" the nucleus together are of interest only for sub-atomic particles and are not the forces that we are typically familiar with in chemistry. Electrostatic (Coulomb's law) would suggest that the potential energy of a He-4 nucleus would be higher than that of the separated particle since the positive protons should repel each other. This is true at long distances, but at very short distances the nuclear strong force becomes dominate. The potential energy of the protons and neutrons at extremely small distances becomes much lower. Thus the nucleus is more stable than the separated particles (for some combinations of protons and neutrons). This energy that "holds" the nucleus together is the binding energy. A different way to think about the binding energy is that it is the amount of energy needed to break up the nucleus into its parts.
\[\rm{^4_2He \rightarrow 2^1_1p + 2^1_0n}\]
The amount of energy required for this "reaction" is the binding energy of the He-4 nucleus. Conversely if we form a helium-4 nucleus from two protons and 2 neutrons this would be the amount of energy that would be released. The difference in mass between the separate particles and the nuclide is called the mass defect. This "missing mass" is in fact the binding energy.
In the same way that in a chemical reaction some bonds are lower in energy than others (more stable) some nuclei are lower in energy than others. The potential energy of the nuclei is related to nuclear strong force and the nuclear weak force. This a topic that is not explored in detail. However, the key idea is simply that some combinations of protons and neutrons have a lower potential energy (more stable) than others. This is exactly the same as some combination of atoms (bonds) being lower in energy than others in a chemical change.
Take for example the following reaction
\[{\rm 2H_2(g) + O_2(g) \rightarrow 2H_2O(g)}\]
This reaction is exothermic, ΔHr° = -484 kJ mol-. That is two water molecules are lower in energy than two hydrogen molecules and one oxygen molecule. Why? The potential energy of the atoms in the water molecules is lower than the atoms in the hydrogen and oxygen molecules. We can calculate this change by calculating the energy required to break the bonds in the reactants and the energy that is gained by forming the bonds in the products. First, all the reactants are broken apart into atoms. Then these atoms are recombined to form the products. This is simply the bond energies of the reactants minus the bond energy of the products.
\[{\rm 2H_2(g) + O_2(g) \xrightarrow{BE_{reactants}} 4H(g) + 2O(g) \xrightarrow{-BE_{products}} 2H_2O(g)}\]
These bond energies could be estimated from bond enthalpy tables or calculated rigorously with quantum mechanics. Finally, this change could be measured in the lab by measuring the enthalpy of the reaction.
This same idea can be applied to nuclear reactions. The difference in energy in the products and reactants is simply the difference in the potential energy of the products compared to the reactants. Take for example the following fission reaction
\[{\rm ^{235}_{92}U + ^1_0n \rightarrow ^{137}_{56}Ba + ^{97}_{36}Kr + 2 ^1_0n}\]
This reaction is extremely exothermic (~1013 J mol-1). This reflects a difference in binding energy of the products compared to the reactants. The combination of Ba-137 and K-97 is more stable than U-235. The transition can be imagined as first breaking up the nuclei into their component parts and then forming the products from the individual protons and neutrons. This the binding energies of the reactants minus the binding energies of the products.
\[{\rm ^{235}_{92}U + ^1_0n \xrightarrow{BE_{reactants}} 92^{1}_{1}p + 144 ^{1}_{0}n \xrightarrow{BE_{products}} ^{137}_{56}Ba + ^{97}_{36}Kr + 2 ^1_0n}\]
Where now BE is the "binding energy" rather than the "bond energy". The binding energy of the two nuclei combined in the products is lower in energy than the one nucleus in the reactants. Thus this reaction releases a large amount of energy.
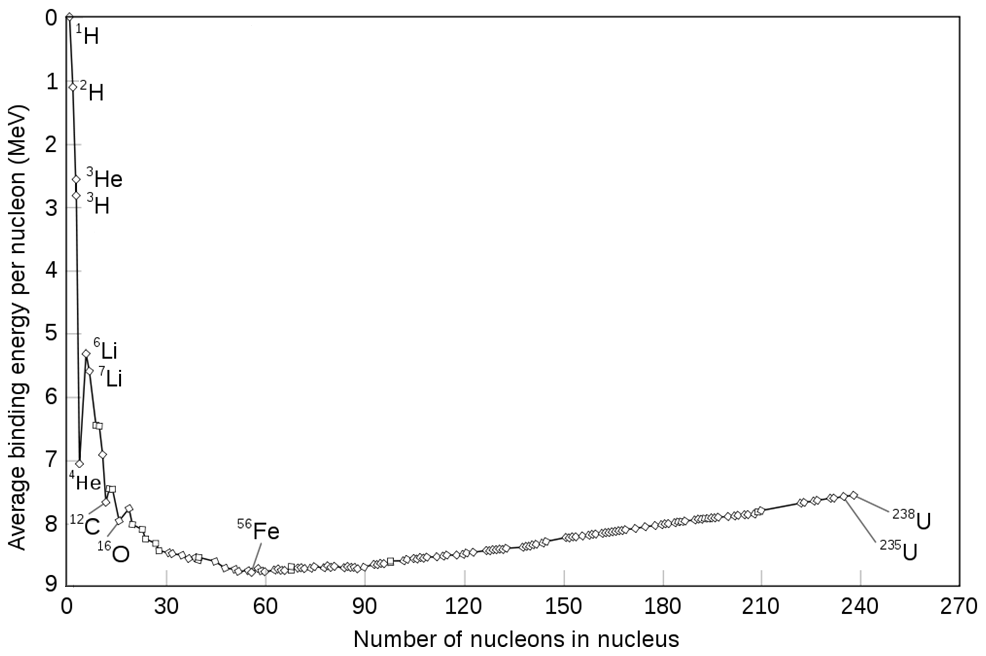
If we were simply to compare the binding energy of nuclei to each other, the largest nuclei would have the highest binding energy since they contain the largest number of protons and neutrons. However, what is of interest is not the total binding energy, but instead the binding energy per nucleon (proton/neutron). The binding energy of nuclei has a particular trend such that the nucleus with the highest binding energy per nucleon (neutron/proton) is iron. Another way to say this is that the most stable (lowest energy) nucleus is iron. Therefore it is downhill in energy for small nuclei to combine to form heavier nuclei if they are lighter than iron. Conversely, it is downhill in energy for larger nuclei to break apart into smaller nuclei for elements heavier than iron. This means that fusion is exothermic for elements lighter than iron, but fission is exothermic for elements heavier than iron. The graph below shows the binding energy per nucleon vs nucleon number (mass number).
© 2013 mccord/vandenbout/labrake